快速傅立叶变换(FFT)与数字信号处理
Oct 17, 2008快速傅立叶变换(FFT)是离散傅立叶变换(DFT)的快速算法, 具体原理我也讲不清楚, 如果你从来没听过这2个词, 你就进错地方了…
FFT最经常的应用就是数字信号处理, 比如你有这样一堆信号:
Matlab代码是这样:
t=linspace(0,2*pi,2^10); % discretizes [0, 2pi] into 256 nodes
y=exp(-(cos(t).^2)).*(sin(2*t)+2*cos(4*t)+0.4*sin(t).*sin(50*t));
画出来是酱紫:
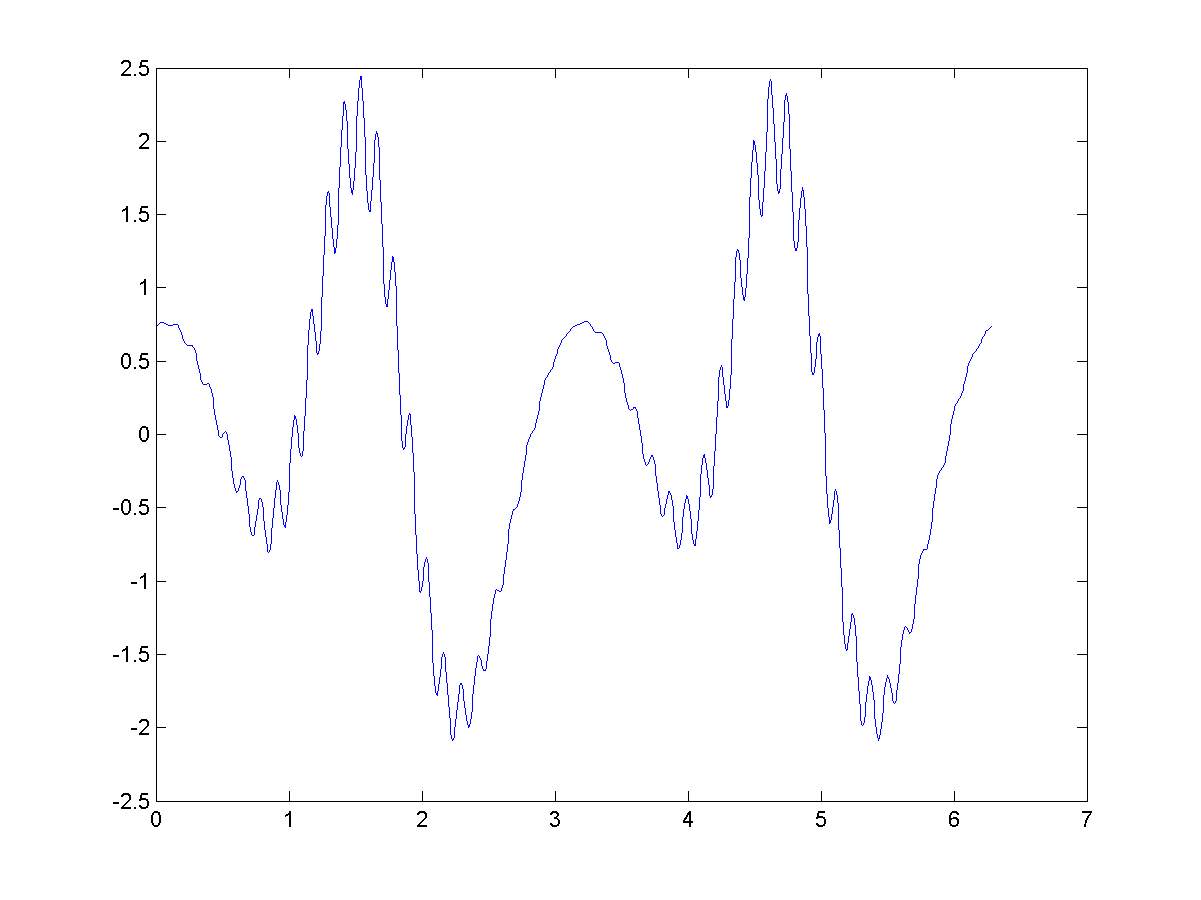
看起来有点混乱, 于是我想过滤掉一些频率, 减少噪声. 比如我想过滤掉所有高频, 只保留最低的6个频率, 那么就需要借助Matlab的函数fft和ifft了. fft就是快速傅立叶变换, 通过一系列信号值求出所有频率; 而ifft是逆向离散傅立叶变换, 即通过频率求信号值.
t=linspace(0,2*pi,2^10); % discretizes [0, 2pi] into 1024 nodes
y=exp(-(cos(t).^2)).*(sin(2*t)+2*cos(4*t)+0.4*sin(t).*sin(50*t));
z=fft(y,2^10);
y1=<span style="font-weight:bold;color:#000080;">if</span>ft([z(1:6) zeros(1,2^10-6*2) z(2^10-5:2^10)],2^10);
y1=real(y1);
plot(t,y)
hold on
plot(t,y1,<span style="color:#0000ff;">'r'</span>),title('Signal filtering with FFT: keeping 6 lowest frequencies'),legend('original signal', 'signal without high frequencies', 'Location', 'SouthOutside')
hold off
要注意的是FFT得到的频率是对称的, 因此保留低频时两端的数据都要.
结果如图:
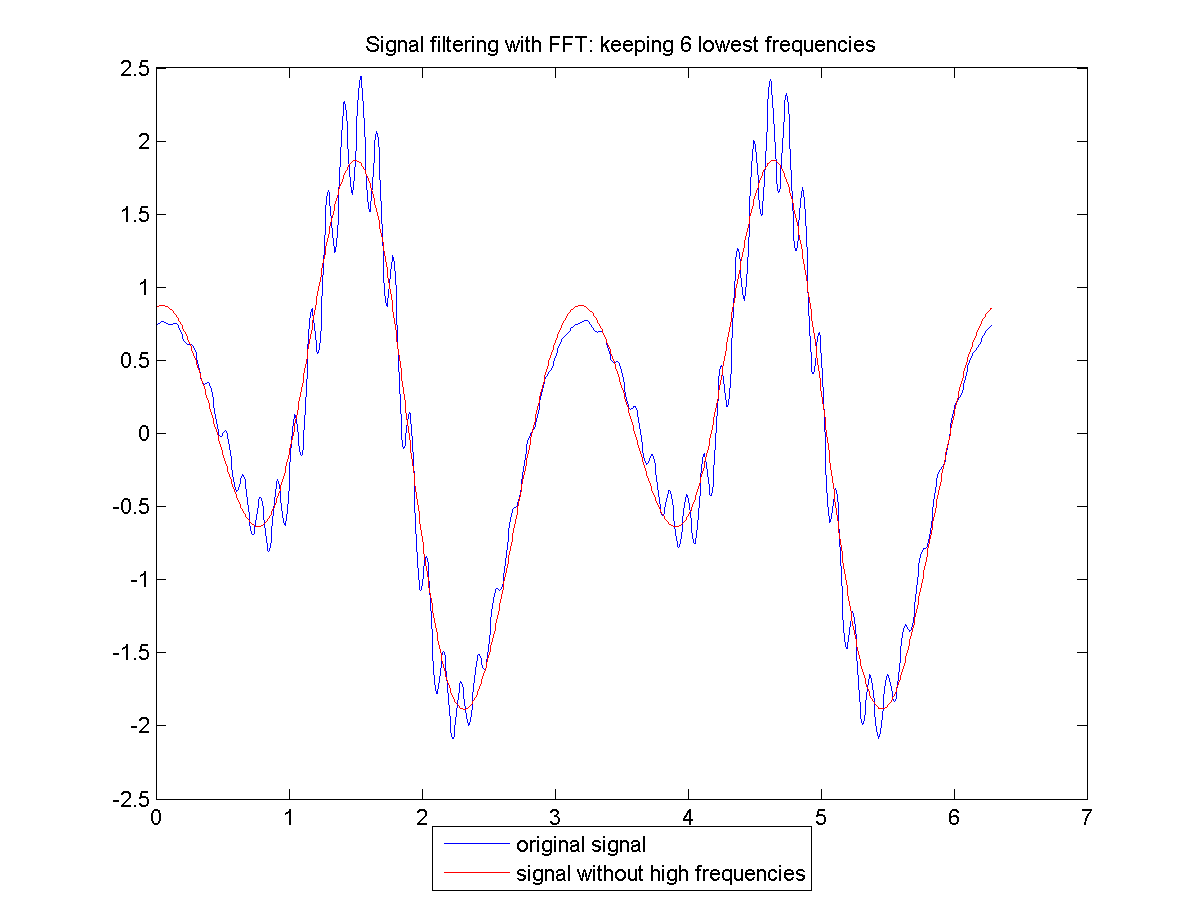
话说是不是平滑一些了?
FFT在信号处理上的另一大应用就是数据压缩. 上面的原始数据有1024个点, 而我们希望仅用20%的数据就能保存下信号的大部分信息, 要怎么办呢?
这个问题我苦思好久, 终于想明白, 我们需要的是把强度(振幅)小的频率去掉(赋0值), 于是用以下代码实现:
t=linspace(0,2*pi,2^10);
y=exp(-t.^2/10).*(sin(2*t)+2*cos(4*t)+0.4*sin(t).*sin(10*t));
r=0.2; %20 percent of the original amount of storage
a=floor(2^10*r);
plot(t,y)
z=fft(y,2^10);
cutoff=sort(abs(z),'descend');
for i=1:length(z)
if abs(z(i))<cutoff(a)
z(i)=0;
end
end
y1=ifft(z,2^10);
y1=real(y1);
plot(t,y)
hold on
plot(t,y1,'r'),title('Signal compression with FFT'),legend('original signal','compressed signal with 20% of original size')
hold off
saveas(1,'prob8b.png');
结果:

除了边缘波动很大以外, 压缩后的信号和原始信号几乎重合!
这就是FFT在网络电视, 高速下载等领域得到广泛应用的原因, 因为这种压缩虽然是有损数据压缩, 会损失一些数据, 但是人眼或人耳几乎是察觉不到的.
ps. 以上是我的期中作业, 具体对不对还要等老师公布答案才知道-.- 仅供参考..
Reference: