《九章算术注》：两千年前计算太阳高度的方法

《九章算术注》是魏晋期间数学家刘徽（约公元225年—295年）为《九章算术》写的注解。序言中有如下段落：

立两表于洛阳之城，令高八尺。南北各尽平地，同日度其正中之景。以景差为法，表高乘表间为实，实如法而一，所得加表高，即日去地也。

这就是中学数学讲的计算太阳高度的方法。如图：

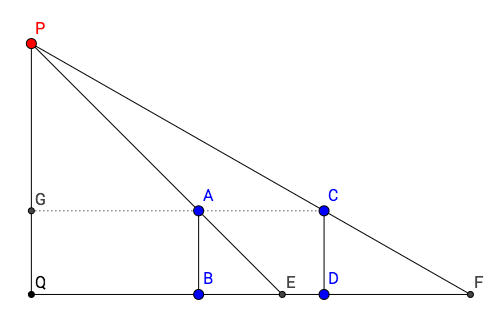
图中 P 是太阳。AB，CD是两根等长旗杆（两表）。AB是旗杆高度（表高）。BD是两根旗杆距离（表间）。两个旗杆投影长度差（影差）为 (DF - BE)。“以景差为法”，意思是 影差 是除数（法）。“表高乘表间为实”，意思是 表高 x 表间 是被除数（实）。“实如法而一”，意思是用被除数（实）除以除数（法）。

则太阳高度（日去地） = 表高 x 表间 / 影差 + 表高

用图中符号表示则是：

PQ = AB x BD / (DF - BE) + AB

用相似三角形容易证明。提示：延长CA交PQ于G，做辅助线CG。下面交给读者你了。^_^

这是《九章算术注》里详细讨论的重差法的一个例子。重差，重复取差之意，是利用两个或两个以上的表当作测量基准的测量方法。神奇的是，中国古代数学理论里并没有相似三角形的概念，而是用勾股比率。

杨辉（约1238年－约1298年）《续古摘奇算法》卷下对勾股比率的解释：

直田之长名股，其阔名勾，于两隅角斜界一线，其名弦。弦之內、外分二勾股，其一勾中容横，其一股中容直，二积之数皆同。

如图：

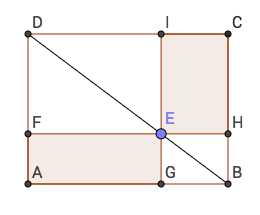
易知矩形AFEG和矩形CHEI面积相等，则 EF x EG = EH x EI，即 DF / EF = EG / BG，我们并不需要利用相似三角形DEF和EBG就推出了同样的两边对应成比例的结论。